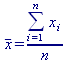,
gdzie n jest liczbą danych.LIBREOFFICE – ARKUSZ KALKULACYJNY CALC
Zadanie 1
Uruchom arkusz kalkulacyjny LibreOffice Calc i wprowadź realne dane (np. wzrost koleżanek i kolegów z grupy) do kolumny A arkusza kalkulacyjnego (opisanej jako xi), a następnie oblicz ich wartość średnią arytmetyczną zdefiniowaną jako:
,
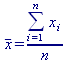gdzie n jest liczbą danych.
W sąsiedniej komórce oblicz wartość średnią arytmetyczną korzystając funkcji statystycznych arkusza kalkulacyjnego LibreOffice Calc xśr (Wstaw → Funkcja → Statystyka → Średnia lub Średnia A). Zaokrąglij otrzymane wyniki stosując zasady zaokrąglania liczb przybliżonych (1 cyfra).
Zadanie 2
Przejdź do nowego arkusza (Arkusz 2) aplikacji LibreOffice Calc i oblicz wartość średnią arytmetyczną następujących trzech rozrzutów liczb: 10 i 60, 0 i 70 oraz 34 i 36. Co można powiedzieć po jakości serii (jak bardzo rozrzucone są analizowane wartości)?
Zadanie 3
Wróć do poprzedniego arkusza (Arkusz 1) i oblicz (uzupełniając odpowiednio kolumny poniższej tabeli) wartość eksperymentalnego odchylenia standardowego (rozrzut wyników serii):
.
|
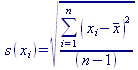A |
B |
C |
D |
E |
F |
G |
... |
... |
... |
|
|
i |
|
xi |
xi - xśr |
|
(xi - xśr)2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
xśr = |
... |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
s(xi) = |
... |
|
|
... |
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
s(xi) = |
... |
|
|
n |
|
|
|
|
|
|
|
|
|
n = |
... |
∑ xi = |
... |
|
∑ (xi – xśr)2 = |
... |
|
|
|
W sąsiedniej komórce, korzystając z funkcji statystycznych arkusza kalkulacyjnego LibreOffice Calc (Wstaw → Funkcja → Statystyka → Odch. Standardowe lub Odch. Standardowe A), oblicz s(xi) charakteryzujące rozrzut wyników serii odchylenie standardowe. Zaokrąglij otrzymane wyniki stosując zasady zaokrąglania liczb przybliżonych (2 cyfry).